library(tidyverse)
library(brms)
polls <- read_csv("https://projects.fivethirtyeight.com/polls-page/data/president_polls_historical.csv")
set.seed(8372)
# set up data, consistent with some other data sources
# this is just national polls
max_size = 5000
matchup = c("Harris", "Trump")
# get just harris-trump matchups
harris_trump <-
polls %>%
group_by(poll_id, question_id) %>%
summarise(all_reps = paste0(answer, collapse = ",") ) %>%
filter(all_reps %in% c("Harris,Trump","Trump,Harris")) %>%
pull(question_id)
# select data
# only national polls where trump-harris are the options
# remove polls that are overlapping
all_polls_df <-
polls %>%
rename(pop = sample_size,
vtype = population) %>%
mutate(begin = as.Date(start_date, "%m/%d/%y"),
end = as.Date(end_date, "%m/%d/%y"),
t = end - (1 + as.numeric(end-begin)) %/% 2,
entry_date = as.Date(created_at, "%m/%d/%y")) %>%
filter(question_id %in% harris_trump,
is.na(state),
!is.na(pollscore),
!is.na(numeric_grade),
answer %in% matchup,
end > as.Date("2024-06-01"),
t >= begin & !is.na(t) & (vtype %in% c("lv","rv","a")),
pop > 1,
pop <= max_size) %>%
mutate(pollster = str_extract(pollster, pattern = "[A-z0-9 ]+") %>% sub("\\s+$", "", .),
pollster = replace(pollster, pollster == "Fox News", "FOX"),
pollster = replace(pollster, pollster == "WashPost", "Washington Post"),
pollster = replace(pollster, pollster == "ABC News", "ABC"),
partisan = ifelse(is.na(partisan), "NP", partisan),
method = case_when(
str_detect(tolower(methodology) ,"online") ~ "online",
str_detect(tolower(methodology) ,"phone") ~ "phone",
TRUE ~ "other"),
week = floor_date(t - days(2), unit = "week") + days(2),
day_of_week = as.integer(t - week),
index_t = 1 + as.numeric(t) - min(as.numeric(t)),
index_w = as.numeric(as.factor(week)),
index_p = as.numeric(as.factor(as.character(pollster))),
n_votes = round(pop * (pct/100))) %>%
distinct(t, pollster, pop, party, .keep_all = TRUE) %>%
select(poll_id, t, begin, end, entry_date, pollster, partisan, numeric_grade, pollscore, vtype, method, pop, n_votes, pct,party,answer, week, day_of_week, starts_with("index_"))
# remove overlapping polls
all_polls_df <-
all_polls_df %>%
group_by(entry_date, pollster, pop, party) %>%
arrange(desc(entry_date), desc(end)) %>%
slice(1)
# drop polls with combined 2-party vote share < 85%
low_vote <-
all_polls_df %>%
group_by(poll_id, entry_date, pollster, pop) %>%
summarise(total_votes = sum(n_votes), .groups = 'drop') %>%
mutate(prop = total_votes / pop) %>%
filter(prop < .85) %>%
select(poll_id, entry_date, pollster, pop)
all_polls_df <- anti_join(all_polls_df, low_vote)
# plot the 2 party pct
all_polls_df %>%
ggplot(aes(x = t, y = pct, color = party)) +
geom_point(aes(size = pop, fill = party),shape = 21, alpha = .2) +
geom_smooth(aes(color = party)) +
scale_color_manual(values = c("#00AEF3","#E81B23")) +
scale_fill_manual(values = c("#00AEF3","#E81B23")) +
scale_y_continuous(limits = c(30, 60)) +
theme_minimal() +
theme(legend.position = 'none')
# RUN MODELS
# -------------------- #
extract_posterior_predictions <- function(x){
# get the median and 95% credible interval
ypred <- posterior_predict(x)
ypred <- apply(ypred, 2, quantile, probs = c(.025, .5, .975)) %>% round()
data.frame(t(ypred)) %>% set_names(c("ymin","median","ymax"))
}
stack_extract_posterior_predictions_naive <- function(x1, x2, weights = c(.5, .5), return = "agg"){
# average weighted predictions from two models
pred1 <- posterior_predict(x1)
pred2 <- posterior_predict(x2)
pred_avg <- (pred1 * weights[1]) + (pred2 * weights[2])
if(return=="agg"){
ypred <- apply(pred_avg, 2, quantile, probs = c(.025, .5, .975)) %>% round()
out <- data.frame(t(ypred)) %>% set_names(c("ymin","median","ymax"))
}
else if(return=="raw"){
out <- pred_avg
}
return(out)
}
stack_extract_posterior_predictions <- function(x1, x2){
# get the median and 95% credible interval
ypred <- pp_average(x1, x2, summary = FALSE)
ypred <- apply(ypred, 2, quantile, probs = c(.025, .5, .975)) %>% round()
data.frame(t(ypred)) %>% set_names(c("ymin","median","ymax"))
}
# politcal idx
dem <- all_polls_df$party == 'DEM'
gop <- all_polls_df$party == 'REP'
# adjust for poll type, partisan
bprior <- c(
prior(normal(0, 0.5), class = 'Intercept'),
prior(normal(0, 0.5), class = 'b'),
prior(student_t(3, 0, 1), class = 'sd')
)
sprior <- c(prior(normal(0, 0.5), class = 'Intercept'),
prior(student_t(3, 0, 1), class = 'sds'))
# rescaled polster weights, mean of 1
W <- all_polls_df$numeric_grade/mean(all_polls_df$numeric_grade, na.rm = TRUE)
W_dem = W[dem]
W_gop = W[gop]
# aggregation model
fit2.1 <-
brm(
n_votes |
trials(pop) + weights(W_dem) ~ 1 + partisan + method + vtype +
(1 | index_t) +
(1 | index_p),
family = "binomial",
data = all_polls_df[dem, ],
data2 = list(W_dem = W_dem),
prior = bprior,
chains = 4,
cores = 4,
file = "data\\election_model\\fit2.1"
)
fit2.2 <-
brm(
n_votes |
trials(pop) + weights(W_gop) ~ 1 + partisan + method + vtype +
(1 | index_t) +
(1 | index_p),
family = "binomial",
data = all_polls_df[gop, ],
data2 = list(W_gop = W_gop),
prior = bprior,
chains = 4,
cores = 4,
file = "data\\election_model\\fit2.2"
)
# using a cubic regression spline for smoothing
fit2.1s <-
brm(n_votes | trials(pop) + weights(W_dem) ~ 1 + s(index_t, bs = 'cr'),
data = all_polls_df[dem, ],
data2 = list(W_dem = W_dem),
family = "binomial",
prior = sprior,
chains = 4,
cores = 4,
control = list(adapt_delta = 0.99),
file = "data\\election_model\\fit2.1s"
)
fit2.2s <-
brm(n_votes |trials(pop) + weights(W_gop) ~ 1 + s(index_t, bs = 'cr'),
data = all_polls_df[gop, ],
family = "binomial",
prior = sprior,
data2 = list(W_gop = W_gop),
chains = 4,
cores = 4,
control = list(adapt_delta = 0.99),
file = "data\\election_model\\fit2.2s"
)
# add predictions back to dataframe with weighted predictions
# weight 1 = hlm, weight 2 = smoothing model
# more weight on #2 = more smoothing
# default is about 40% hlm, 60% smoothing
weights = c(.4, .6)
pred_dem <- cbind.data.frame(stack_extract_posterior_predictions_naive(fit2.1, fit2.1s, weights = weights), all_polls_df[dem,])
pred_gop <- cbind.data.frame(stack_extract_posterior_predictions_naive(fit2.2, fit2.2s, weights = weights), all_polls_df[gop,])
test <-
rbind.data.frame(pred_dem, pred_gop) %>%
mutate(across(ymin:ymax, function(x)
(x / pop)*100)) %>%
group_by(party, end) %>%
summarise(across(ymin:ymax, mean)) %>%
ungroup()
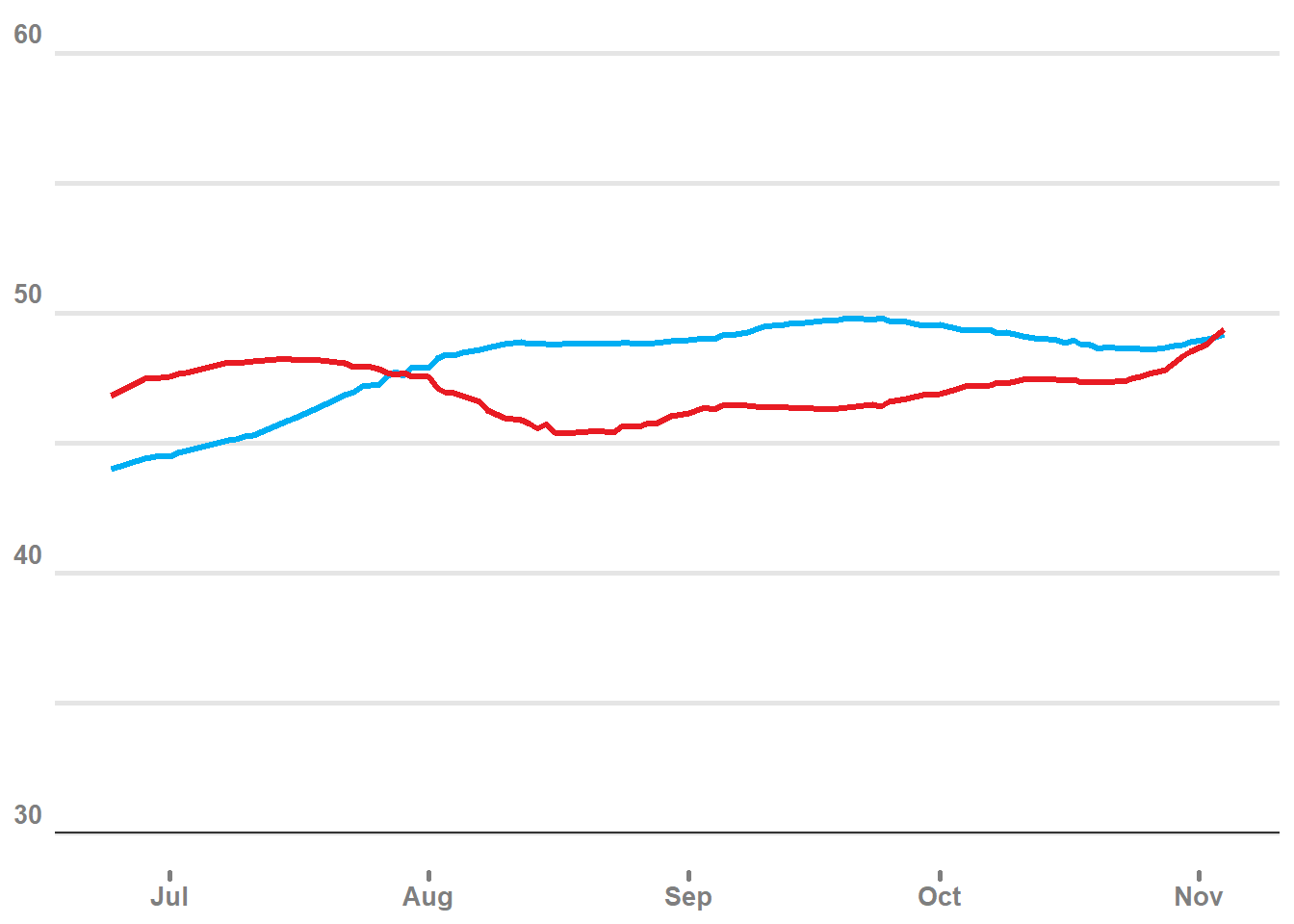
plot1<-
test %>%
group_by(party, end) %>%
summarise(across(ymin:ymax, mean)) %>%
ggplot(aes(x = end)) +
geom_line(aes(y = median, group = party, color = party), linewidth = 1.2) +
scale_color_manual(values = c("#00AEF3","#E81B23")) +
scale_fill_manual(values = c("#00AEF3","#E81B23")) +
scale_y_continuous(limits = c(30, 60)) +
geom_hline(yintercept = 30, color = 'grey20') +
theme_minimal() +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank(),
panel.grid.major.y = element_line(color = "grey90", linewidth = 1 ),
panel.grid.minor.y = element_line(color = "grey90", linewidth = 1),
axis.ticks.x = element_line(lineend = "round", linewidth = 1, color = 'grey50'),
axis.title = element_blank(),
axis.text = element_text(size = 10, color = 'grey50', face = 'bold'),
axis.text.y = element_text(vjust = -0.5))
plot1
# labels for end points
end_labels <- test %>%
filter(end == max(end)) %>%
group_by(party) %>%
slice(1)
# w/o error bars
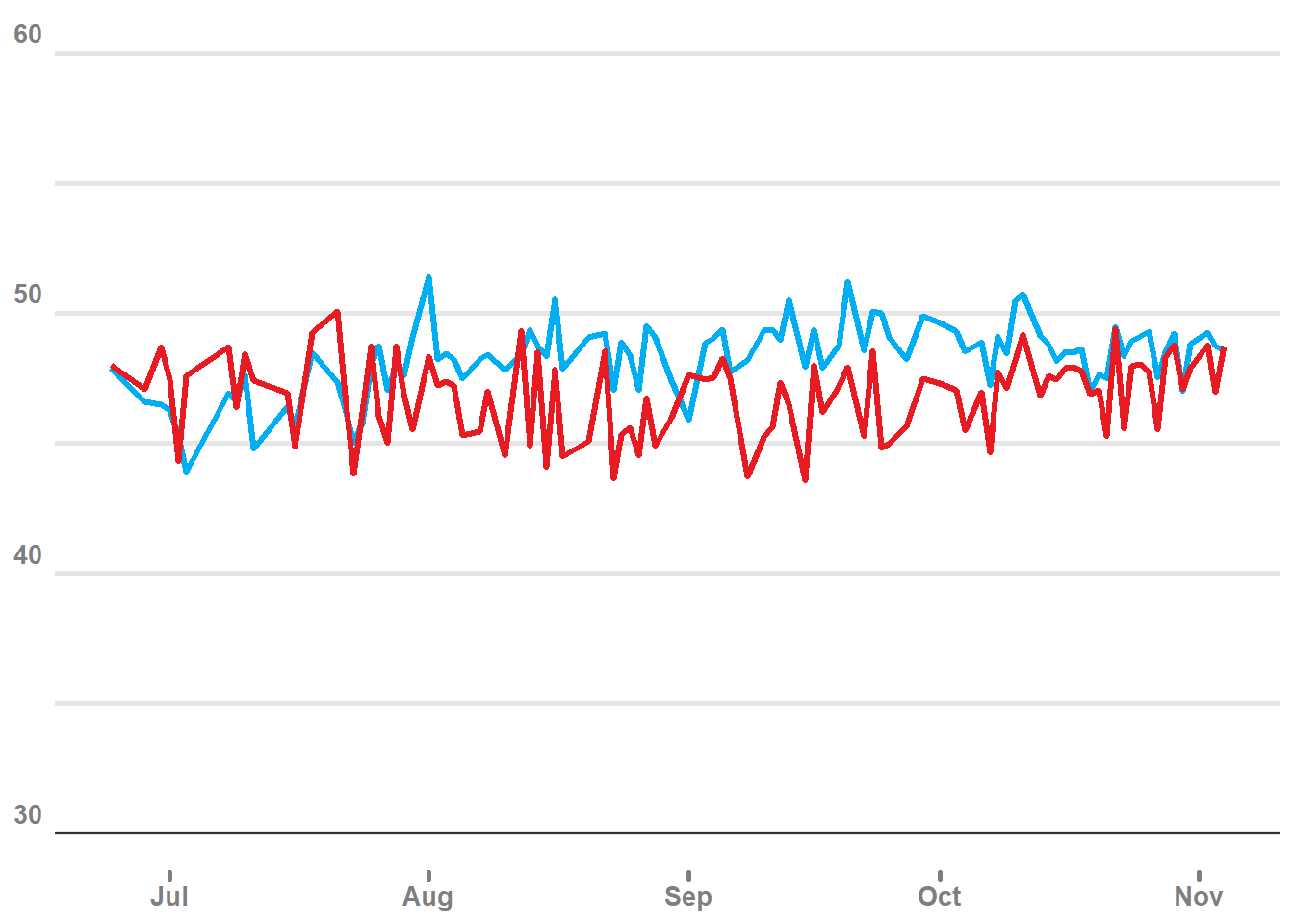
plot1 +
geom_point(data = all_polls_df, aes(x = end, y = pct, color = party, fill = party), shape = 21, size = 2, alpha = .2)
# add point sizes and label
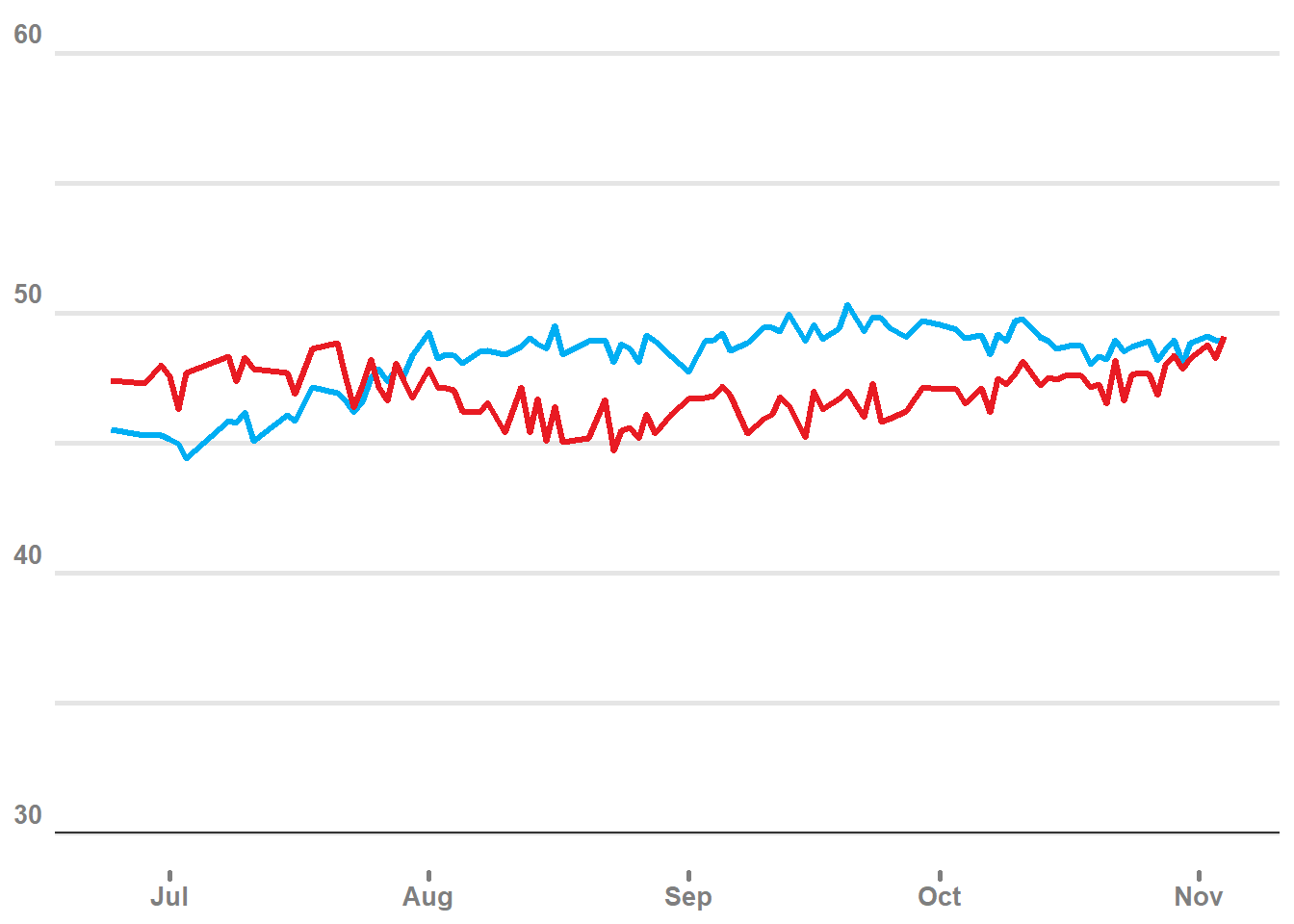
plot1 +
geom_point(data = all_polls_df, aes(x = end, y = pct, color = party, fill = party, size = pop), alpha = .2) +
geom_point(data = end_labels, aes(x = end, y = median, color = party), size = 2.5) +
geom_label(data = end_labels, aes(x = end, y = median, label = round(median,1), fill = party), color = 'white', fontface = 'bold', nudge_x = 5, nudge_y = c(-.75,.75), size = 3.2)
# facet plots
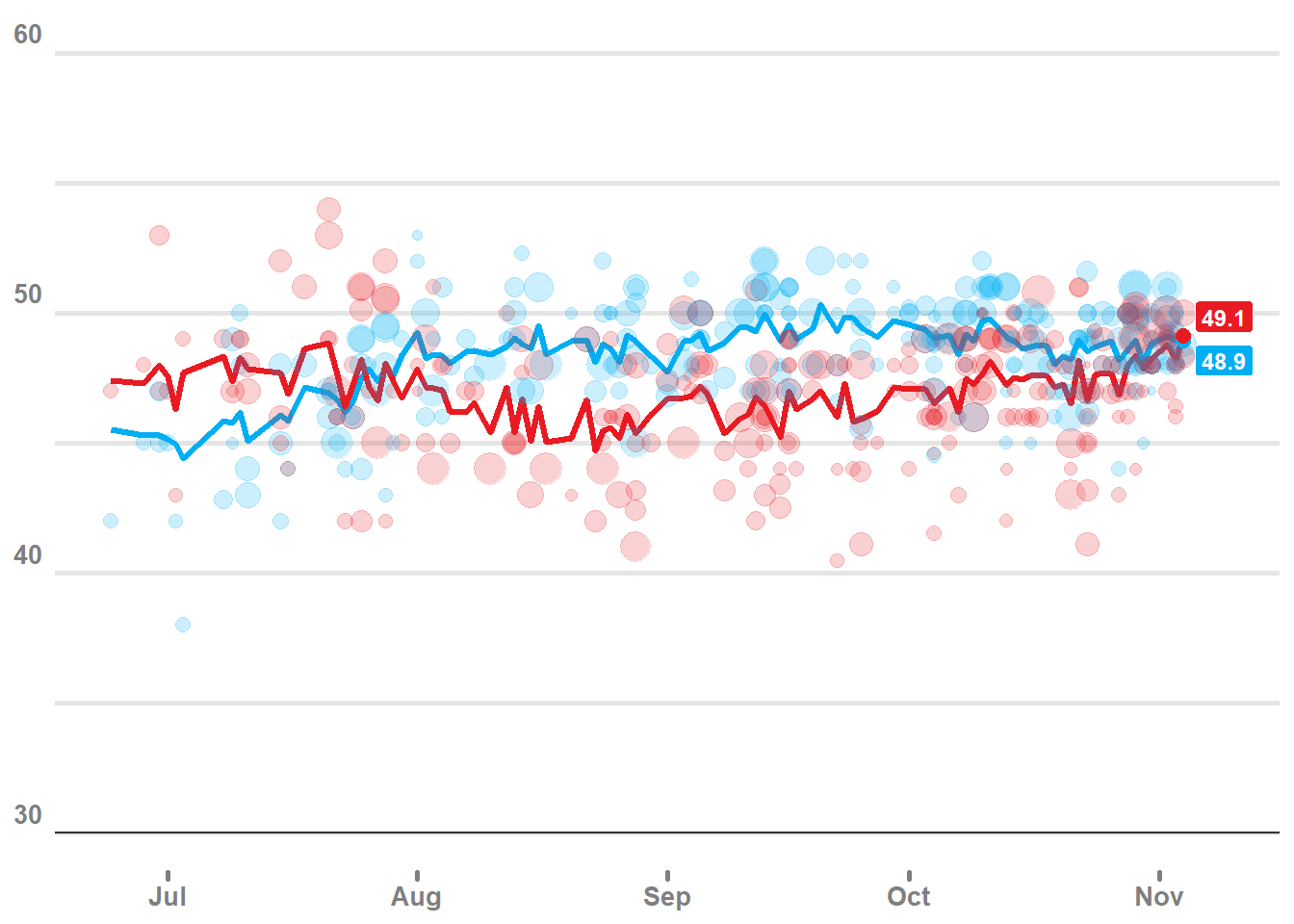
plot1 +
geom_point(data = all_polls_df, aes(x = end, y = pct, color = party, fill = party, size = pop), alpha = .2) +
geom_ribbon(aes(ymin = ymin, ymax = ymax, group = party, fill = party), color = 'white', alpha = .2)
# difference on max data
raw_dem <- stack_extract_posterior_predictions_naive(fit2.1, fit2.1s, weights = weights, return = "raw")
raw_gop <- stack_extract_posterior_predictions_naive(fit2.2, fit2.2s, weights = weights, return = "raw")
# compute dem margin based on most recent 10 days worth of polls
dem_margin <- raw_dem / (raw_dem + raw_gop)
max_date <- max(pred_dem$end)
date_idx <- seq.Date(from = max_date,by = "-1 day",length.out = 10)
T <- as.numeric(rownames(pred_dem[pred_dem$end %in% date_idx, ]))
mean(apply(dem_margin[,T], 1, function(x) mean(x > .5)))
# 95% CI and mean
# predicted share of 2-party vote
mean(apply(dem_margin[,T], 1, quantile, probs = c(0.025)))
mean(apply(dem_margin[,T], 1, mean))
mean(apply(dem_margin[,T], 1, quantile, probs = c(0.975)))
# predicted % times that dem candidate wins popular vote
# NOT the same as winning the election !!!
mean(dem_margin[,T] > .5)
hist(dem_margin)
Comments